ELETROMAGNETISMO
Um condutor de cobre de 180 cm de comprimento e percorrido por uma corrente de 13 A e faz um ângulo de 35 graus com um campo magnético uniforme de 1,5 T. Determine aproximadamente a força magnética em N sobre o condutor.
33,58
14,56
20,13
10,23
40,56
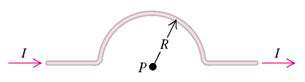
Na figura abaixo determine o módulo do campo magnético resultante em T, produzido no ponto P pela corrente que passa na seção semicircular do fio indicado. (Dica calcule o campo de uma espira e depois dívida por dois), considere i = 2 A e R = 0,5 
m e a constante de permibialidade igual a
4. 
7
1.10-2
2.10-7
4.10-7
3.10-8
6.10-8
Determine a intensidade da divergência no campo vetorial a seguir:
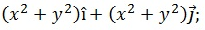
nos pontos:
(x,y) = ( 2;1)
3
2
8
1
6
No campo vetorial abaixo calcule o rotacional:
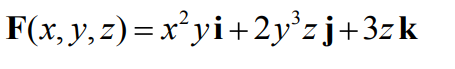
-5y3i -x3k
-4y5i -xk
-8y2i -x3k
-2y3i -x2k
-9y2i -x7k
Temos uma esfera condutora de 15 cm de raio e potencial de 200 V, sendo o potencial elétrico no infinito igual a 200 V,
calcule aproximadamente a carga dessa esfera. Considere a constante eletrostática igual a 8,99 × 109 N.m2/C2
7,89 mC
5,6 mC
10mC
5,69C
3,3nC
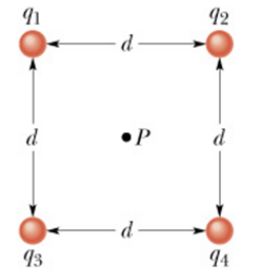
Calcule aproximadamente o potencial elétrico em volts, resultante no ponto P, considere que no infinito o potencial vale zero, sabendo que o valor das cargas valem, q1 = +12 nC, q2 = -24 nC , q3 = +31 nC q4= +17 nC,
considere o valor da distancia d = 130 cm e a constante eletrostática igual a 9.109 N.m2/C2
Sa
150
350
300
400
200
Um disco de raio 10 cm está orientado de modo que seu vetor normal faça um ângulo de 30° com o campo elétrico uniforme de módulo 2 x 103 N/C.
Calcule aproximadamente o fluxo do campo elétrico em N.m2 /C no disco?
54
70
32
90
15
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 4 x 106 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 5 x 105 N m²/C
Duas esferas puntiformes de 1 mC e -2 mC localizadas em (3, 2, -1) e (-1, -1, 4), respectivamente. Calcule aproximadamente a força sobre uma esfera de 10 nC, localizada em (0, 3, 1). Considere a constante eletrostática igual a 
N.m²/c².
F = ( -26,507i -13,817j +7,506 k) mN
F = ( -16,507i -13,817j +17,506 k) mN
F = ( i +817j +7,506 k) mN
F = ( -6,507i -3,817j +7,506 k) mN
F = ( -12,507i -8,817j +7,506 k) mN
Determine aproximadamente a distância entre duas esferas eletrizadas com cargas iguais a Q1 = 26 μC e Q2= −47 μC para que a força eletrostática entre elas tenha módulo 5,7 N. considere a constante eletrostática igual a 
N.m²/c².
33,58
14,56
20,13
10,23
40,56
Na figura abaixo determine o módulo do campo magnético resultante em T, produzido no ponto P pela corrente que passa na seção semicircular do fio indicado. (Dica calcule o campo de uma espira e depois dívida por dois), considere i = 2 A e R = 0,5 m e a constante de permibialidade igual a
4. 7
1.10-2
2.10-7
4.10-7
3.10-8
6.10-8
Determine a intensidade da divergência no campo vetorial a seguir:
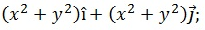
nos pontos:
(x,y) = ( 2;1)
3
2
8
1
6
No campo vetorial abaixo calcule o rotacional:
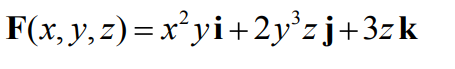
-5y3i -x3k
-4y5i -xk
-8y2i -x3k
-2y3i -x2k
-9y2i -x7k
Temos uma esfera condutora de 15 cm de raio e potencial de 200 V, sendo o potencial elétrico no infinito igual a 200 V,
calcule aproximadamente a carga dessa esfera. Considere a constante eletrostática igual a 8,99 × 109 N.m2/C2
7,89 mC
5,6 mC
10mC
5,69C
3,3nC
Calcule aproximadamente o potencial elétrico em volts, resultante no ponto P, considere que no infinito o potencial vale zero, sabendo que o valor das cargas valem, q1 = +12 nC, q2 = -24 nC , q3 = +31 nC q4= +17 nC,
considere o valor da distancia d = 130 cm e a constante eletrostática igual a 9.109 N.m2/C2
Sa
150
350
300
400
200
Um disco de raio 10 cm está orientado de modo que seu vetor normal faça um ângulo de 30° com o campo elétrico uniforme de módulo 2 x 103 N/C.
Calcule aproximadamente o fluxo do campo elétrico em N.m2 /C no disco?
54
70
32
90
15
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 4 x 106 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 5 x 105 N m²/C
Duas esferas puntiformes de 1 mC e -2 mC localizadas em (3, 2, -1) e (-1, -1, 4), respectivamente. Calcule aproximadamente a força sobre uma esfera de 10 nC, localizada em (0, 3, 1). Considere a constante eletrostática igual a N.m²/c².
F = ( -26,507i -13,817j +7,506 k) mN
F = ( -16,507i -13,817j +17,506 k) mN
F = ( i +817j +7,506 k) mN
F = ( -6,507i -3,817j +7,506 k) mN
F = ( -12,507i -8,817j +7,506 k) mN
Determine aproximadamente a distância entre duas esferas eletrizadas com cargas iguais a Q1 = 26 μC e Q2= −47 μC para que a força eletrostática entre elas tenha módulo 5,7 N. considere a constante eletrostática igual a N.m²/c².
1.10-2
2.10-7
4.10-7
3.10-8
6.10-8
Determine a intensidade da divergência no campo vetorial a seguir:
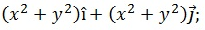
nos pontos:
(x,y) = ( 2;1)
3
2
8
1
6
No campo vetorial abaixo calcule o rotacional:
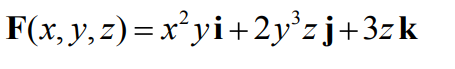
-5y3i -x3k
-4y5i -xk
-8y2i -x3k
-2y3i -x2k
-9y2i -x7k
Temos uma esfera condutora de 15 cm de raio e potencial de 200 V, sendo o potencial elétrico no infinito igual a 200 V,
calcule aproximadamente a carga dessa esfera. Considere a constante eletrostática igual a 8,99 × 109 N.m2/C2
7,89 mC
5,6 mC
10mC
5,69C
3,3nC
Calcule aproximadamente o potencial elétrico em volts, resultante no ponto P, considere que no infinito o potencial vale zero, sabendo que o valor das cargas valem, q1 = +12 nC, q2 = -24 nC , q3 = +31 nC q4= +17 nC,
considere o valor da distancia d = 130 cm e a constante eletrostática igual a 9.109 N.m2/C2
Sa
150
350
300
400
200
Um disco de raio 10 cm está orientado de modo que seu vetor normal faça um ângulo de 30° com o campo elétrico uniforme de módulo 2 x 103 N/C.
Calcule aproximadamente o fluxo do campo elétrico em N.m2 /C no disco?
54
70
32
90
15
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 4 x 106 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 5 x 105 N m²/C
Duas esferas puntiformes de 1 mC e -2 mC localizadas em (3, 2, -1) e (-1, -1, 4), respectivamente. Calcule aproximadamente a força sobre uma esfera de 10 nC, localizada em (0, 3, 1). Considere a constante eletrostática igual a N.m²/c².
F = ( -26,507i -13,817j +7,506 k) mN
F = ( -16,507i -13,817j +17,506 k) mN
F = ( i +817j +7,506 k) mN
F = ( -6,507i -3,817j +7,506 k) mN
F = ( -12,507i -8,817j +7,506 k) mN
Determine aproximadamente a distância entre duas esferas eletrizadas com cargas iguais a Q1 = 26 μC e Q2= −47 μC para que a força eletrostática entre elas tenha módulo 5,7 N. considere a constante eletrostática igual a N.m²/c².
3
2
8
1
6
No campo vetorial abaixo calcule o rotacional:
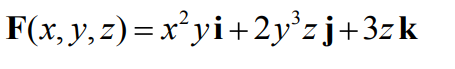
-5y3i -x3k
-4y5i -xk
-8y2i -x3k
-2y3i -x2k
-9y2i -x7k
Temos uma esfera condutora de 15 cm de raio e potencial de 200 V, sendo o potencial elétrico no infinito igual a 200 V,
calcule aproximadamente a carga dessa esfera. Considere a constante eletrostática igual a 8,99 × 109 N.m2/C2
7,89 mC
5,6 mC
10mC
5,69C
3,3nC
Calcule aproximadamente o potencial elétrico em volts, resultante no ponto P, considere que no infinito o potencial vale zero, sabendo que o valor das cargas valem, q1 = +12 nC, q2 = -24 nC , q3 = +31 nC q4= +17 nC,
considere o valor da distancia d = 130 cm e a constante eletrostática igual a 9.109 N.m2/C2
Sa
150
350
300
400
200
Um disco de raio 10 cm está orientado de modo que seu vetor normal faça um ângulo de 30° com o campo elétrico uniforme de módulo 2 x 103 N/C.
Calcule aproximadamente o fluxo do campo elétrico em N.m2 /C no disco?
54
70
32
90
15
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 4 x 106 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 5 x 105 N m²/C
Duas esferas puntiformes de 1 mC e -2 mC localizadas em (3, 2, -1) e (-1, -1, 4), respectivamente. Calcule aproximadamente a força sobre uma esfera de 10 nC, localizada em (0, 3, 1). Considere a constante eletrostática igual a N.m²/c².
F = ( -26,507i -13,817j +7,506 k) mN
F = ( -16,507i -13,817j +17,506 k) mN
F = ( i +817j +7,506 k) mN
F = ( -6,507i -3,817j +7,506 k) mN
F = ( -12,507i -8,817j +7,506 k) mN
Determine aproximadamente a distância entre duas esferas eletrizadas com cargas iguais a Q1 = 26 μC e Q2= −47 μC para que a força eletrostática entre elas tenha módulo 5,7 N. considere a constante eletrostática igual a N.m²/c².
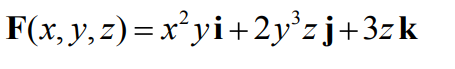
-5y3i -x3k
-4y5i -xk
-8y2i -x3k
-2y3i -x2k
-9y2i -x7k
Temos uma esfera condutora de 15 cm de raio e potencial de 200 V, sendo o potencial elétrico no infinito igual a 200 V,
calcule aproximadamente a carga dessa esfera. Considere a constante eletrostática igual a 8,99 × 109 N.m2/C2
7,89 mC
5,6 mC
10mC
5,69C
3,3nC
Calcule aproximadamente o potencial elétrico em volts, resultante no ponto P, considere que no infinito o potencial vale zero, sabendo que o valor das cargas valem, q1 = +12 nC, q2 = -24 nC , q3 = +31 nC q4= +17 nC,
considere o valor da distancia d = 130 cm e a constante eletrostática igual a 9.109 N.m2/C2
Sa
150
350
300
400
200
Um disco de raio 10 cm está orientado de modo que seu vetor normal faça um ângulo de 30° com o campo elétrico uniforme de módulo 2 x 103 N/C.
Calcule aproximadamente o fluxo do campo elétrico em N.m2 /C no disco?
54
70
32
90
15
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 4 x 106 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 5 x 105 N m²/C
Duas esferas puntiformes de 1 mC e -2 mC localizadas em (3, 2, -1) e (-1, -1, 4), respectivamente. Calcule aproximadamente a força sobre uma esfera de 10 nC, localizada em (0, 3, 1). Considere a constante eletrostática igual a N.m²/c².
F = ( -26,507i -13,817j +7,506 k) mN
F = ( -16,507i -13,817j +17,506 k) mN
F = ( i +817j +7,506 k) mN
F = ( -6,507i -3,817j +7,506 k) mN
F = ( -12,507i -8,817j +7,506 k) mN
Determine aproximadamente a distância entre duas esferas eletrizadas com cargas iguais a Q1 = 26 μC e Q2= −47 μC para que a força eletrostática entre elas tenha módulo 5,7 N. considere a constante eletrostática igual a N.m²/c².
7,89 mC
5,6 mC
10mC
5,69C
3,3nC
Calcule aproximadamente o potencial elétrico em volts, resultante no ponto P, considere que no infinito o potencial vale zero, sabendo que o valor das cargas valem, q1 = +12 nC, q2 = -24 nC , q3 = +31 nC q4= +17 nC,
considere o valor da distancia d = 130 cm e a constante eletrostática igual a 9.109 N.m2/C2
Sa
150
350
300
400
200
Um disco de raio 10 cm está orientado de modo que seu vetor normal faça um ângulo de 30° com o campo elétrico uniforme de módulo 2 x 103 N/C.
Calcule aproximadamente o fluxo do campo elétrico em N.m2 /C no disco?
54
70
32
90
15
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 4 x 106 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 5 x 105 N m²/C
Duas esferas puntiformes de 1 mC e -2 mC localizadas em (3, 2, -1) e (-1, -1, 4), respectivamente. Calcule aproximadamente a força sobre uma esfera de 10 nC, localizada em (0, 3, 1). Considere a constante eletrostática igual a N.m²/c².
F = ( -26,507i -13,817j +7,506 k) mN
F = ( -16,507i -13,817j +17,506 k) mN
F = ( i +817j +7,506 k) mN
F = ( -6,507i -3,817j +7,506 k) mN
F = ( -12,507i -8,817j +7,506 k) mN
Determine aproximadamente a distância entre duas esferas eletrizadas com cargas iguais a Q1 = 26 μC e Q2= −47 μC para que a força eletrostática entre elas tenha módulo 5,7 N. considere a constante eletrostática igual a N.m²/c².
150
350
300
400
200
Um disco de raio 10 cm está orientado de modo que seu vetor normal faça um ângulo de 30° com o campo elétrico uniforme de módulo 2 x 103 N/C.
Calcule aproximadamente o fluxo do campo elétrico em N.m2 /C no disco?
54
70
32
90
15
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 4 x 106 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 5 x 105 N m²/C
Duas esferas puntiformes de 1 mC e -2 mC localizadas em (3, 2, -1) e (-1, -1, 4), respectivamente. Calcule aproximadamente a força sobre uma esfera de 10 nC, localizada em (0, 3, 1). Considere a constante eletrostática igual a N.m²/c².
F = ( -26,507i -13,817j +7,506 k) mN
F = ( -16,507i -13,817j +17,506 k) mN
F = ( i +817j +7,506 k) mN
F = ( -6,507i -3,817j +7,506 k) mN
F = ( -12,507i -8,817j +7,506 k) mN
Determine aproximadamente a distância entre duas esferas eletrizadas com cargas iguais a Q1 = 26 μC e Q2= −47 μC para que a força eletrostática entre elas tenha módulo 5,7 N. considere a constante eletrostática igual a N.m²/c².
54
70
32
90
15
Sabendo que uma carga elétrica de 1.8 µC está situada no centro de uma superfície gaussiana cúbica de 55 cm de aresta. Calcule aproximadamente a intensidade do fluxo elétrico através desta superfície. Considere a constante eletrostática igual a 8, 99 · 109 Nm2/C2 .
ΦE = 2 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 4 x 106 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 5 x 105 N m²/C
Duas esferas puntiformes de 1 mC e -2 mC localizadas em (3, 2, -1) e (-1, -1, 4), respectivamente. Calcule aproximadamente a força sobre uma esfera de 10 nC, localizada em (0, 3, 1). Considere a constante eletrostática igual a N.m²/c².
F = ( -26,507i -13,817j +7,506 k) mN
F = ( -16,507i -13,817j +17,506 k) mN
F = ( i +817j +7,506 k) mN
F = ( -6,507i -3,817j +7,506 k) mN
F = ( -12,507i -8,817j +7,506 k) mN
Determine aproximadamente a distância entre duas esferas eletrizadas com cargas iguais a Q1 = 26 μC e Q2= −47 μC para que a força eletrostática entre elas tenha módulo 5,7 N. considere a constante eletrostática igual a N.m²/c².
ΦE = 2 x 105 N m²/C
ΦE = 7 x 103 N m²/C
ΦE = 4 x 106 N m²/C
ΦE = 12 x 105 N m²/C
ΦE = 5 x 105 N m²/C
Duas esferas puntiformes de 1 mC e -2 mC localizadas em (3, 2, -1) e (-1, -1, 4), respectivamente. Calcule aproximadamente a força sobre uma esfera de 10 nC, localizada em (0, 3, 1). Considere a constante eletrostática igual a N.m²/c².
F = ( -26,507i -13,817j +7,506 k) mN
F = ( -16,507i -13,817j +17,506 k) mN
F = ( i +817j +7,506 k) mN
F = ( -6,507i -3,817j +7,506 k) mN
F = ( -12,507i -8,817j +7,506 k) mN
Determine aproximadamente a distância entre duas esferas eletrizadas com cargas iguais a Q1 = 26 μC e Q2= −47 μC para que a força eletrostática entre elas tenha módulo 5,7 N. considere a constante eletrostática igual a N.m²/c².
N.m²/c².F = ( -26,507i -13,817j +7,506 k) mN
F = ( -16,507i -13,817j +17,506 k) mN
F = ( i +817j +7,506 k) mN
F = ( -6,507i -3,817j +7,506 k) mN
F = ( -12,507i -8,817j +7,506 k) mN
Determine aproximadamente a distância entre duas esferas eletrizadas com cargas iguais a Q1 = 26 μC e Q2= −47 μC para que a força eletrostática entre elas tenha módulo 5,7 N. considere a constante eletrostática igual a N.m²/c².
N.m²/c².